Data Representation (binary, Two’s Complement, Floating Point)
Category: COMPUTER SCIENCE | 29th October 2025, Wednesday
In The World Of Digital Computing, data Representation is The Foundation That Enables Computers To Store, Process, And Communicate Information. Unlike Humans, Who Work With Decimal Numbers And Letters, Computers Operate Entirely On Binary Signals—combinations Of Zeros And Ones. Every Form Of Data, Whether Numerical, Textual, Or Graphical, Is Encoded Into Binary Form Before Processing. Understanding How Data Is Represented In Binary, Two’s Complement, And Floating-point Formats Is Essential For Grasping How Computers Perform Arithmetic Operations, Manage Memory, And Maintain Precision.
Binary Representation
Binary Representation Is The Simplest And Most Fundamental Form Of Data Encoding In Digital Systems. In This System, Only Two Digits—0 and 1—are Used To Represent Information. Each Binary Digit, Or bit, Corresponds To A Power Of Two. For Example, The Binary Number 1011 represents The Decimal Value (1×2³) + (0×2²) + (1×2¹) + (1×2?) = 8 + 0 + 2 + 1 = 11. Unlike The Decimal System That Uses Base 10, Binary Is A base-2 Numeral System, Which Makes It Ideal For Computers That Depend On Two Electrical States: On (1) And Off (0).
In Binary, The Concept Of bit Grouping Is Essential. Eight Bits Make Up One byte, Which Is The Most Common Unit Of Digital Storage. Larger Data Units Include Kilobytes (KB), Megabytes (MB), Gigabytes (GB), And Terabytes (TB). Textual Data Is Often Stored Using Binary Codes Such As ASCII (American Standard Code For Information Interchange) Or Unicode, Where Each Character Corresponds To A Specific Binary Value. For Instance, The Letter “A” In ASCII Is Represented As 01000001 in Binary.
Binary Representation Allows Computers To Perform Logical And Arithmetic Operations With Remarkable Speed And Reliability. All Higher-level Operations—like Addition, Subtraction, Multiplication, And Division—are Reduced To Sequences Of Binary Manipulations Performed By Electronic Circuits Known As logic Gates.
Two’s Complement Representation
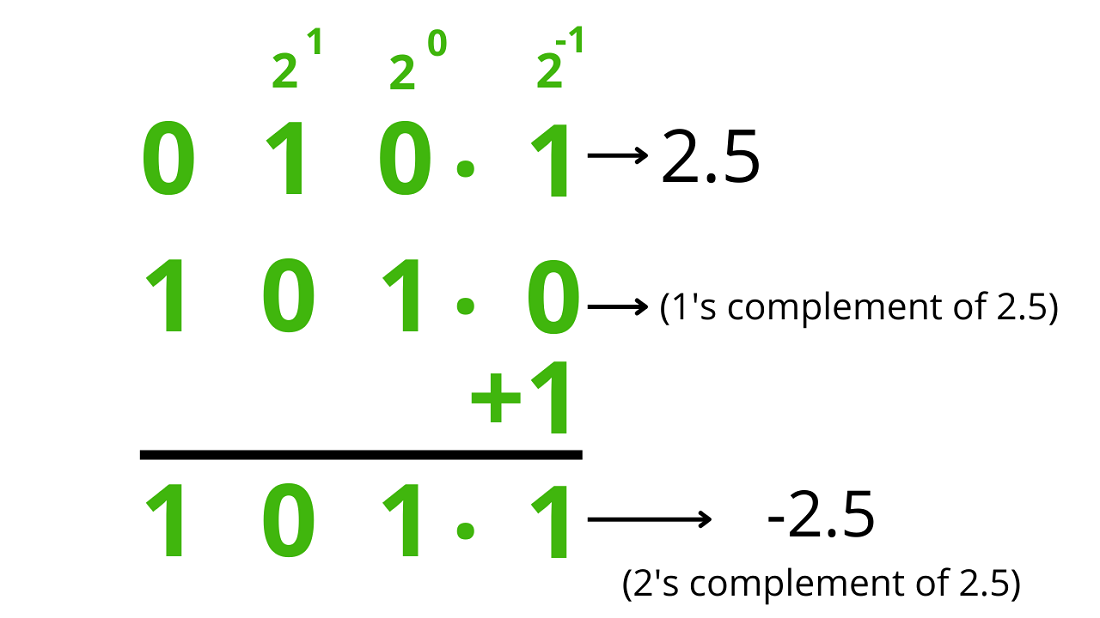
While Binary Representation Works Perfectly For Positive Integers, Representing negative Numbers Introduces Complexity. Early Computing Systems Used Various Methods Like sign-magnitude or one’s Complement Representations, But Both Had Limitations, Such As Ambiguous Zero Values Or Complicated Arithmetic. To Overcome These Problems, Modern Systems Use two’s Complement Representation, Which Is The Standard Method For Encoding Signed Integers In Binary Form.
In Two’s Complement, The Most Significant Bit (MSB) Acts As The sign Bit. If The MSB Is 0, The Number Is Positive; If It Is 1, The Number Is Negative. To Find The Two’s Complement Of A Binary Number, We Follow Two Steps:
1. Invert All Bits (change 0s To 1s And 1s To 0s).
2. Add 1 to The Result.
For Example, To Find The Two’s Complement Of 00001010 (which Represents +10 In Binary), We First Invert It To Get 11110101, And Then Add 1, Resulting In 11110110, Which Represents -10.
The Beauty Of Two’s Complement Lies In Its Simplicity For Arithmetic Operations. Using This Method, Addition And Subtraction Can Be Performed Without Special Rules For Negative Numbers—the Same Circuitry Handles Both Positive And Negative Values Seamlessly. Moreover, There Is Only One Representation For Zero, Avoiding The Dual-zero Problem Found In One’s Complement.
The range Of Numbers That Can Be Represented Depends On The Number Of Bits Used. For Example, In An 8-bit Two’s Complement System, The Range Is From -128 To +127, Since The First Bit Is Reserved For The Sign. Similarly, A 16-bit System Covers -32,768 To +32,767, And A 32-bit System Spans -2,147,483,648 To +2,147,483,647. This Efficient Representation Ensures That Digital Processors Can Perform Integer Arithmetic Quickly And Correctly.
Floating Point Representation
While Integers Are Important, Computers Also Need To Handle real Numbers—values That Include Fractions And Very Large Or Very Small Magnitudes, Such As 3.14159, 0.000125, Or 2.5×10?. Representing Such Numbers Precisely In Binary Requires A System Similar To scientific Notation used In Mathematics. This Is Where floating-point Representation comes Into Play.
In Floating-point Format, A Number Is Expressed As:
± Mantissa × Base^Exponent
Here, The mantissa (also Called The Significand) Represents The Significant Digits, And The exponent Determines The Position Of The Decimal (or Binary) Point. For Binary Floating-point Numbers, The Base Is Always 2.
For Example, The Decimal Number 6.25 Can Be Represented In Binary As 1.1001 × 2². Floating-point Allows The “point” To Move, Or “float,” To Accommodate Very Large Or Very Small Values, Hence The Name.
Modern Computers Follow The IEEE 754 Standard for Floating-point Representation. This Standard Defines Two Primary Formats:
- Single Precision (32-bit)
- Double Precision (64-bit)
In The 32-bit Single Precision Format, 1 Bit Is Used For The Sign, 8 Bits For The Exponent, And 23 Bits For The Mantissa. The Exponent Is Stored In biased Form, Meaning A Bias (usually 127) Is Added To The Actual Exponent Value To Ensure All Exponents Are Non-negative In Storage. For Example, An Exponent Of -3 Is Stored As 124 (since 124 = 127 - 3). The 64-bit Double Precision format Follows A Similar Principle But Allocates 11 Bits For The Exponent And 52 Bits For The Mantissa, Providing Much Greater Accuracy And Range.
Floating-point Arithmetic Is Crucial For Scientific Computation, Graphics, Engineering Simulations, And Financial Modeling. However, It Also Introduces rounding Errors And precision Limits, As Not All Decimal Fractions Can Be Represented Exactly In Binary. For Instance, Numbers Like 0.1 in Decimal Become Repeating Binary Fractions, Leading To Small But Sometimes Significant Rounding Errors In Calculations. Programmers Must Be Aware Of These Limitations When Working With Floating-point Numbers.
Comparison And Importance
Each Of These Data Representation Methods—binary, Two’s Complement, And Floating Point—serves A Unique Purpose In Digital Computation. Binary Is The Universal Foundation That Underlies All Forms Of Data, From Numbers To Characters And Multimedia. Two’s Complement Enables Efficient Handling Of Signed Integers, Allowing Both Positive And Negative Arithmetic Without Complex Circuitry. Floating-point Representation Extends Computational Capability To Real Numbers, Providing The Flexibility And Precision Needed For Scientific And Engineering Applications.
In Modern Computing Systems, Processors, Memory Units, And Compilers Are Optimized To Work Seamlessly With These Representations. Understanding Them Is Vital For Programmers, Hardware Designers, And Computer Scientists Alike, As Even Small Misunderstandings Can Lead To Logical Errors, Data Overflow, Or Precision Loss. From Storing A Simple Integer To Simulating Planetary Motion, Data Representation Remains The Invisible Backbone Of All Computation.
Conclusion
In Essence, data Representation Defines How Abstract Human Concepts Like Numbers And Text Are Translated Into The Digital Language Of Computers. Binary Representation Forms The Core Of This System, Serving As The Basis For All Computation. Two’s Complement Extends Binary Logic To Signed Integers, Simplifying Arithmetic And Hardware Design, While floating-point Representation enables The Expression Of Real Numbers With Vast Ranges And Precise Scaling. Together, These Systems Allow Computers To Perform Complex Mathematical, Scientific, And Logical Operations Accurately And Efficiently. Without Them, The Modern Digital World—from Smartphones To Supercomputers—would Simply Not Function.
Tags:
Data Representation (binary, Two’s Complement, Floating Point)
